逻辑蕴含
2022年06月15日 06:44
专业的逻辑书上说,“蕴含”即→,即可推出,可理解为日常用语的”如果···,那么···“句式.好,现在我说,A蕴含B,即A是B的充分条件
如果“天气冷”蕴含“穿棉袄”,那就说明从“天气冷”可以必然地推出“穿棉袄”,或者说有“天气冷”这一条件,就必有“穿棉袄”这一结果.高中数学中的“小充分,大必要”也是这个意思.如果小集合真包含于大集合,那么一旦知道一个元素属于小集合,也就能必然地推出该元素属于大集合,而这种必然地推出关系正是蕴含.反过来,大推小就不是蕴含了,因为这种推理不是必然的.所以,并不是小推大不具有合理性,而是从小可以必然地得出大,这就是蕴含.简单地说,“蕴含”就是“必然地得出”.
命题逻辑的规则
- 八条整推规则
- 肯定前件:P→Q,P,∴Q
- 否定后件:P→Q,¬Q,∴¬P
- 否定析取支:PVQ,¬P,∴Q
- 化简:P∧Q,∴P;P∧Q,∴Q
- 合取:P,Q,∴P∧Q
- 假言三段论:P→Q,Q→R,∴P→R
- 二难推论:P→Q。R→S,PVR,∴QVS
- 附加:P,∴PVQ;Q,∴PVQ
- 十条置换规则
- 交换:P∨Q→Q∨P;P∧Q→Q∧P
- 双否:P↔¬¬P
- 德摩根律:¬(P∨Q)↔¬P∧¬Q 和 ¬(P∧Q)↔¬P∨¬Q
- 假言易位:(P→Q)↔(¬Q→¬P)
- 蕴含:(P→Q)↔(¬P∨Q)
- 重言:P↔P∨P;P↔P∧P
- 结合:P∨(Q∨R) ↔ (P∨Q)∨R;P∧(Q∧R) ↔ (P∧Q)∧R
- 分配:P∨(Q∧R) ↔ (P∨Q)∧(P∨R);P∧(Q∨R) ↔ (P∧Q)∨(P∧R)
- 移出:(P∧Q→R) ↔ (P→(Q→R))
- 等值:(P↔Q)↔(P→Q) ∧ (Q→P)
- 条件证明规则
- 间接证明规则
直言命题
全称肯定命题:A 全称否定命题:E 特称肯定命题:I 特称否定命题:O
AE,IO,先看全称特称在看肯定否定。二分法,这样记忆或许好点
换质法:两个具有相同主项的直言命题可以相互置换:它们的联项相反,谓项互为补词项。
换位法:主项和谓项交换位置的两个E命题可以相互置换;主项和谓项交换位置的两个I命题可以相互置换
根据换位法,“所有S不是P” 等值于 “所有P不是S”。“有S是P” 等值于 “有P是S”。
根据矛盾关系,“所有S是P”等值于“并非有S不是P”。“有S不是P”等值于“并非你所有S是P”。“所有S不是P”等值于“并非有S是P”。“有S是P”等值于“并非所有S不是P”。
三段论的基本特征:由2三个直言命题组成,其中两个直言命题是前提,另一个直言命题是结论。就主项和谓项而言,三段论包含三个不同的词项。
三段论的词项,小项:作为结论的主项的词项。大项:作为结论的谓项的词项。中项:在两个前提中都出现的词项。
三段论的格:由中项位置不同而形成的各种三段论的形式。

三段论的格与式:三段论任何一格都有64个式,四个格共有256个式。 三段论的式:三段论的式一共有256个,只有15个是有效的。
 词项的周延:一个命题中的一个词项的周延的,当且仅当,这个命题断定了这个词项的全部外延。
词项的周延:一个命题中的一个词项的周延的,当且仅当,这个命题断定了这个词项的全部外延。
根据词项周延的定义
- 全称命题的主项是周延的
- 特称命题的主项是不周延的
- 否定命题的谓项是周延的
- 肯定命题的谓项是不周延的
三段论规则
- 中项至少在一个前提中周延
- 如果一个词项在结论中周延,那么它必须在前提中周延。
- 至少一个前提是肯定的。
- 结论是否定的,当且仅当,有一前提是肯定的。
- 如果两个前提都是全程的,那么结论不能是特称的。
检验三段论的两种方法:文恩图方法、规则方法 强化三段论的检验方法有两种,文恩图方法需要在图中画出主项存在的含义;规则检验法需要去掉规则等等第五条。 日常语言中的直言命题一般都有主项存在的含义,因而,日常语言中的三段论一般都是强化三段论。
全程命题没有主项存在的含义
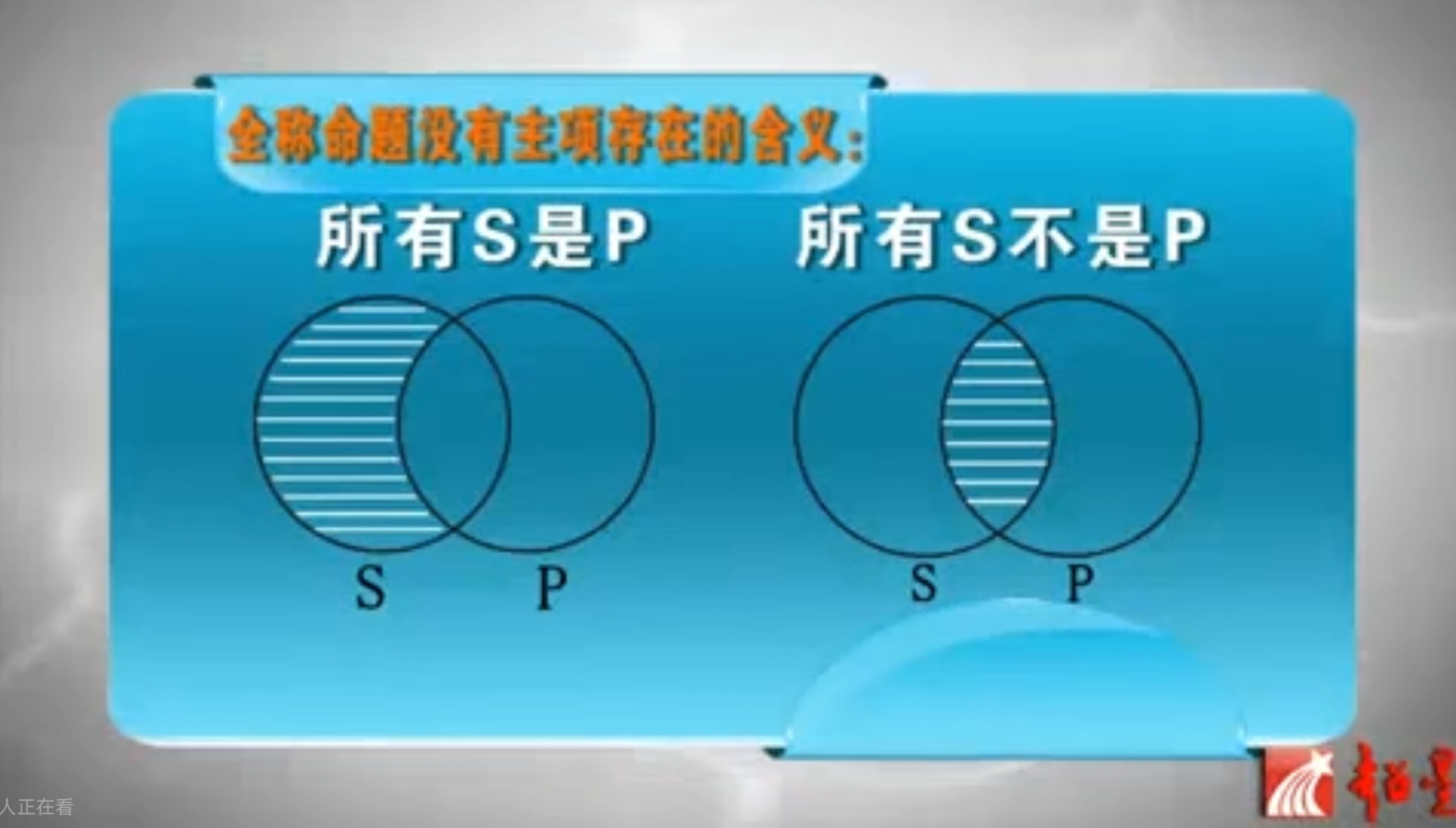
在日常语言里,全程命题有主项存在的含义,在文恩图方法里,全程命题没有主项存在的含义。 在日常语言中,由于全称命题有主项存在的含义,所以由全称命题可以推出存在命题。
强化三段论——全称命题有主项存在的含义。 基本三段论——全称命题没有主项存在的含义。
强化三段论与基本三段论的关系可以理解为:符号+补丁=日常语言。
如果逻辑解决不了这个问题的话,我们宁愿抛弃逻辑,捍卫直觉。就像笛卡尔说的 在这个问题上我们脑子非常清晰它的有效性,我们没有理由放弃直觉啦,放弃的是与我们直觉相伪的所谓的逻辑。最后的根据还是直觉 —陈晓平